Map과 Hash Table

Map은 배열 다음으로 가장 많이 접하는 자료구조인 것 같습니다. 개발을 할때는 물론이고 알고리즘 풀이를 할 때도 Map을 사용하면 쉽게 풀리는 문제가 많습니다.

Map 자료구조의 중요성이 매우 강조되는 만큼 본 포스트에선 Map의 개념과 Hash Table의 동작 원리를 깊게 파악하고자 합니다.

Map

Map이란, key-value 쌍을 저장하는 추상 자료구조 입니다. 같은 key를 가지는 pair는 최대 한 개만 존재해야 합니다. 즉, key는 중복될 수 없고 unique합니다. 반면, value는 중복될 수 있습니다.

Map이 활용되는 예시는 전화번호부 입니다.

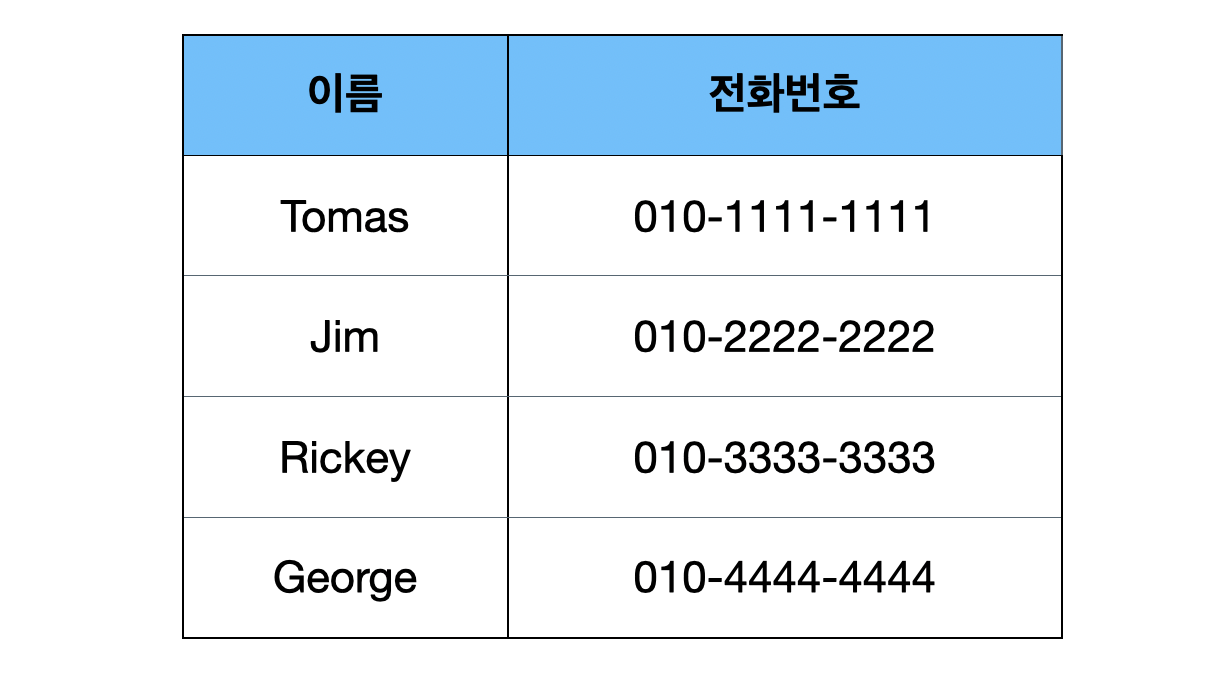
이름을 key, 전화번호를 value로 저장하여 전화번호를 굳이 외우지 않더라도 이름만으로 쉽게 전화번호를 알 수 있습니다.

그리고 counting을 위해 많이 사용됩니다. 알고리즘 풀이를 하다보면 숫자가 무작위로 중복없이 담긴 배열에서 숫자들의 개수를 얻어야 할 때가 많은데요, 이때 Map을 자주 사용합니다.

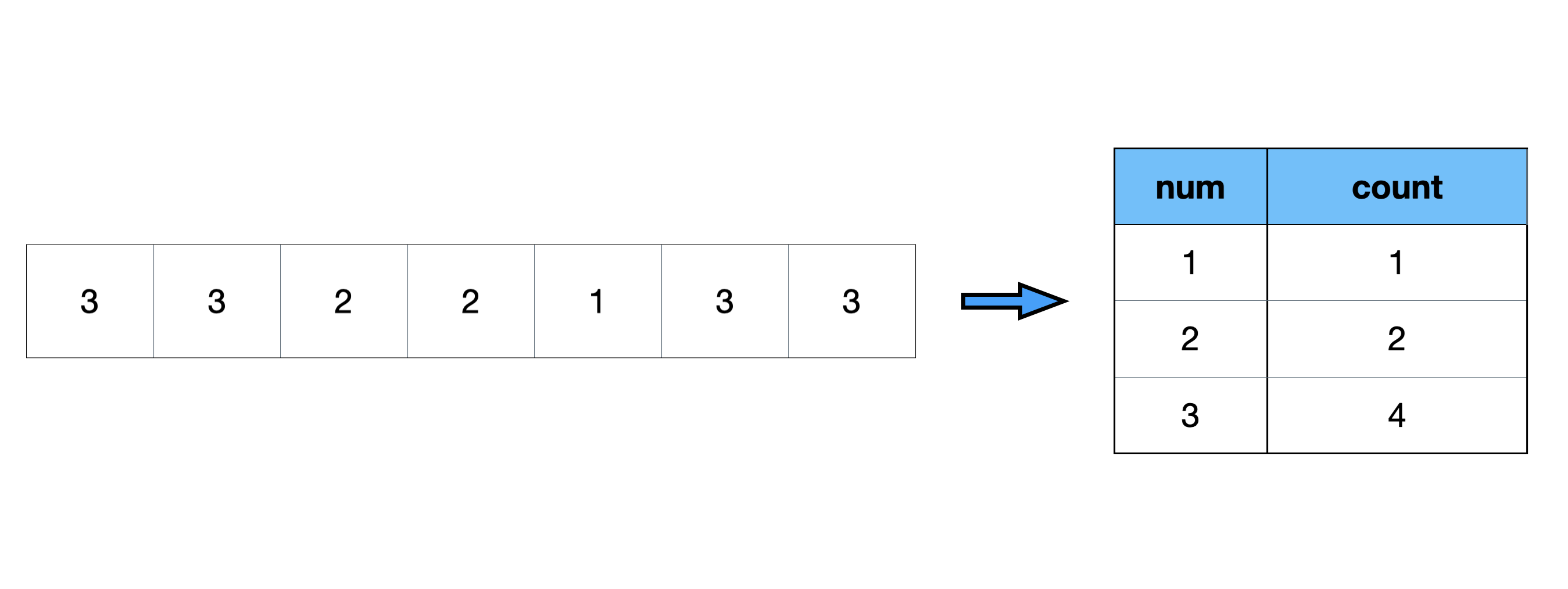
Hash Table

Hash Table이란 배열과 해시 함수를 사용하여 map을 구현한 자료 구조 입니다. 추상 자료 구조인 우선순위 큐를 heap으로 직접 구현하는 것처럼 Map과 Hash Table도 마찬가지 입니다. 일반적으로 상수 시간으로 데이터에 접근하기 때문에 아주 빠릅니다.

앞서 언급한 해시 함수는 임의의 크기를 가지는 type의 데이터를 고정된 크기를 가지는 type의 데이터로 변환하는 함수입니다. Hash Table에서 사용하는 **해시 함수**는 임의의 데이터를 정수로 변환하는 함수입니다. 여기서 임의의 데이터는 전화번호부의 ‘이름’처럼 Hash Table의 key값입니다. 그리고 해시 함수를 거쳐 나온 정수 값을 Hash라고 부릅니다.

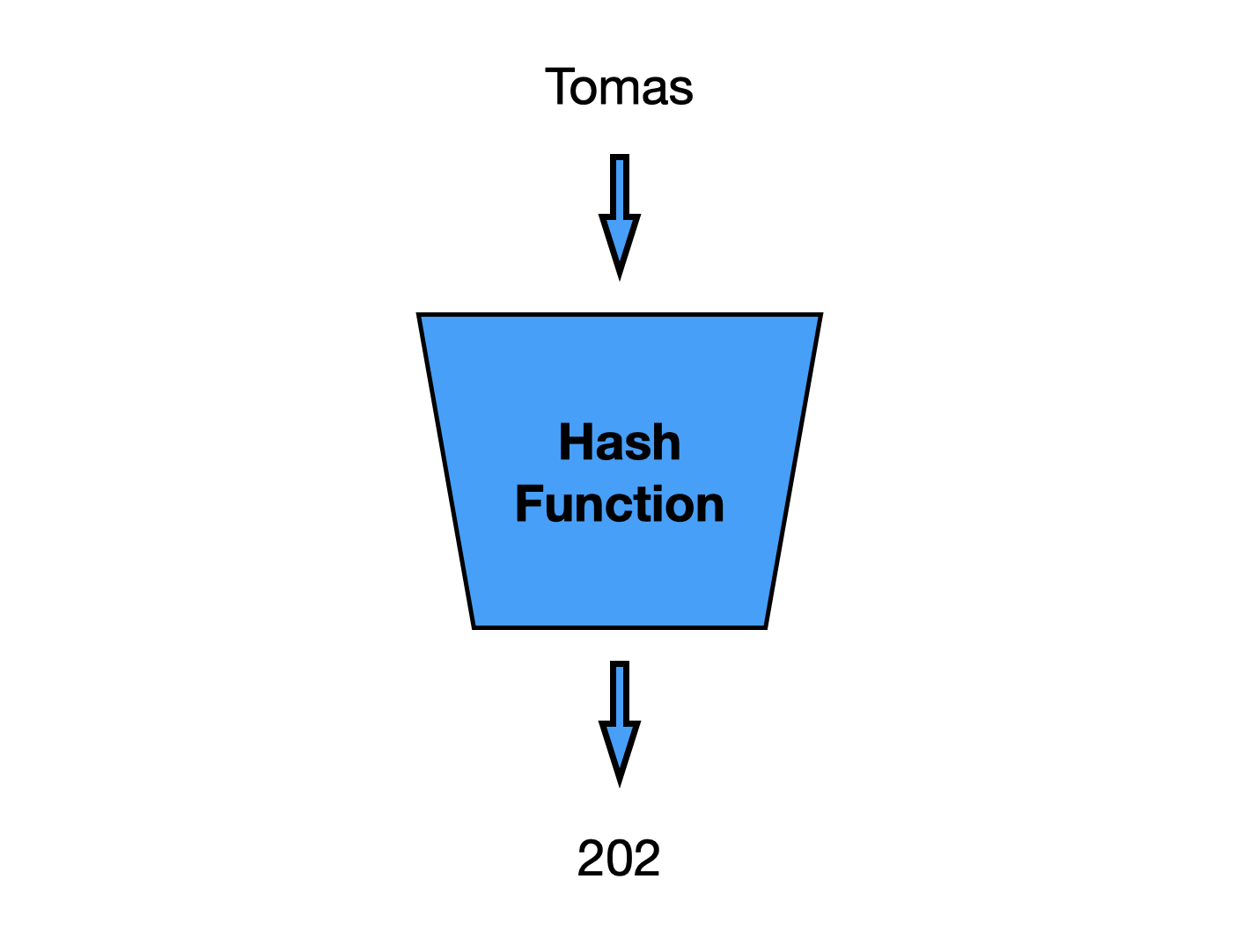
Hash Table의 동작 과정

이제 전화번호 데이터를 가지고 Hash Table이 동작하는 과정을 살펴보겠습니다.

그 전에 용어를 짚고 넘어가겠습니다. Bucket은 배열에서 실질적으로 데이터가 저장되는 각각의 공간을 의미합니다. Capacity는 이 배열의 크기입니다. 그림에서는 배열의 capacity가 8입니다.

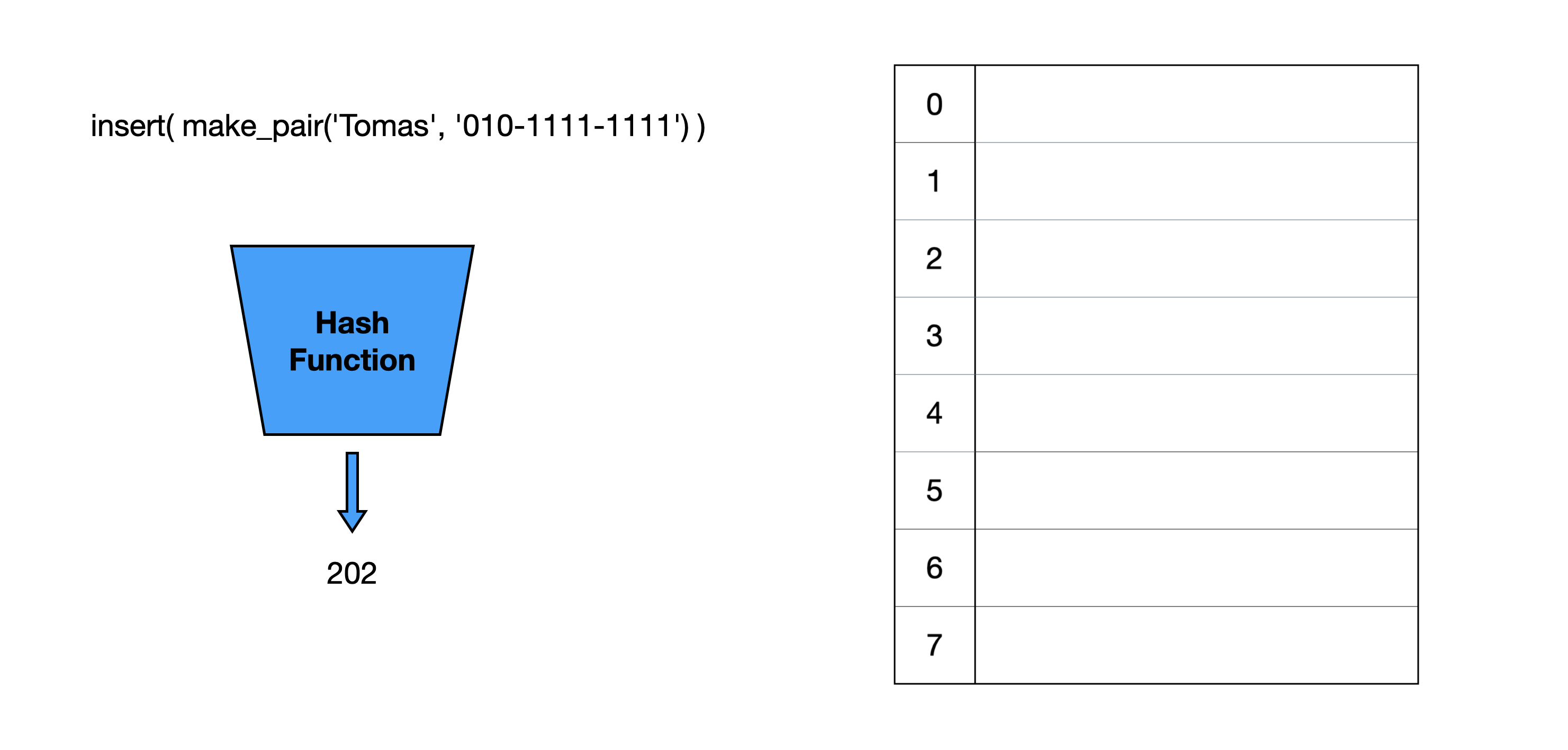
key가 ‘Tomas’, value가 ‘010-1111-1111’인 pair를 해시 테이블에 삽입하겠습니다. 그러나 해시함수의 반환값이 capacity 8보다 큰 202입니다. 배열 인덱스 안에 넣기 위해선 주로 해시값에 모듈러 연산을 수행해야 합니다.

capacity인 8로 모듈러 연산을 수행해 배열 index 2에 데이터가 저장된 것을 확인할 수 있습니다. 그러나, 배열에 value값만 저장해도 괜찮을까요?

Tomas의 전화번호만 저장된 상태에서 저장되어있지 않은 Jim의 연락처를 얻는 과정을 살펴봅시다.

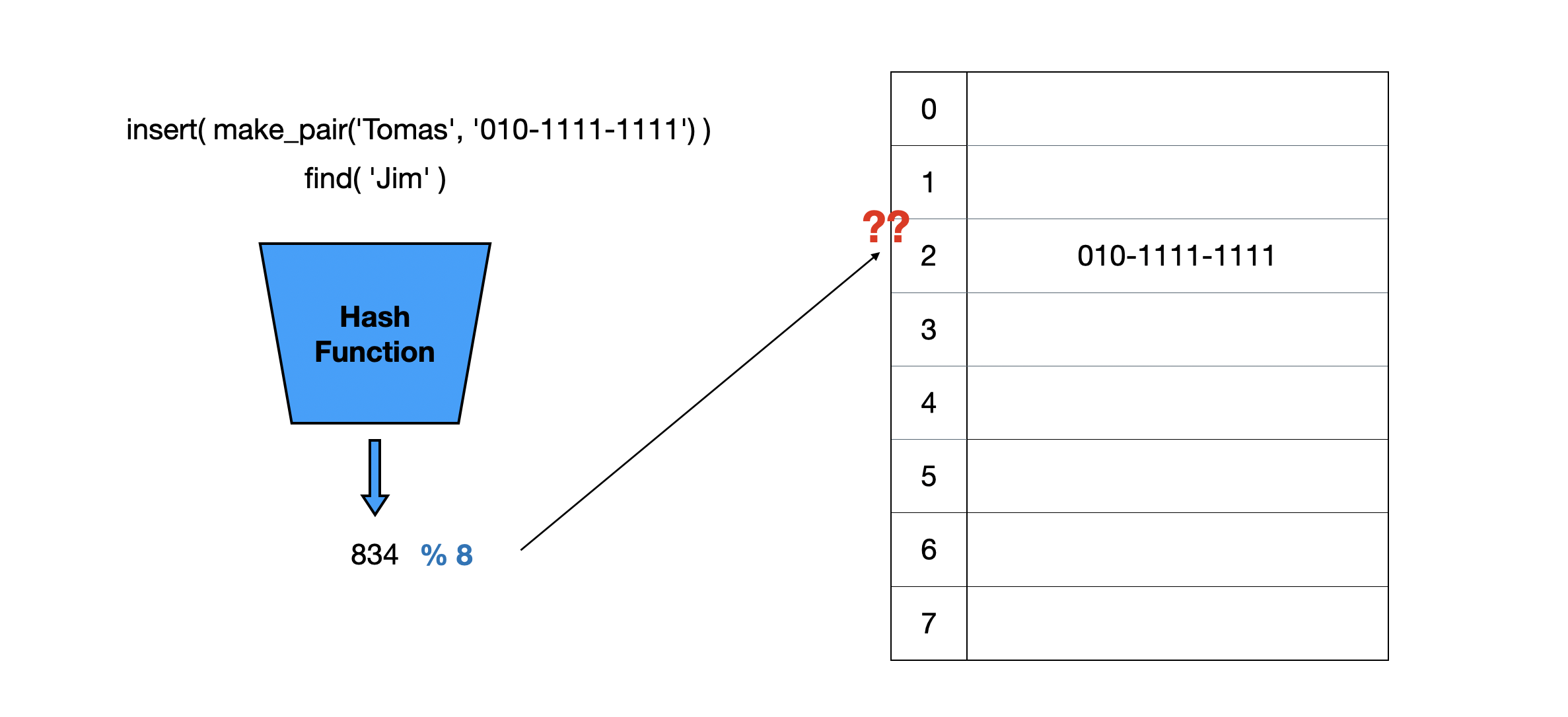
Jim에 대한 해시 함수와 모듈러 연산을 수행한 결과 Tomas와 똑같은 결과인 2가 도출됐습니다. 따라서 배열의 2 index를 조회하게 되는데 Tomas의 전화번호를 만나게 됩니다. value만 저장하게 된다면 내가 찾고자하는 값이 맞는지 확인할 방법이 없기 때문에 다음처럼 key와 value를 같이 저장해야 합니다.

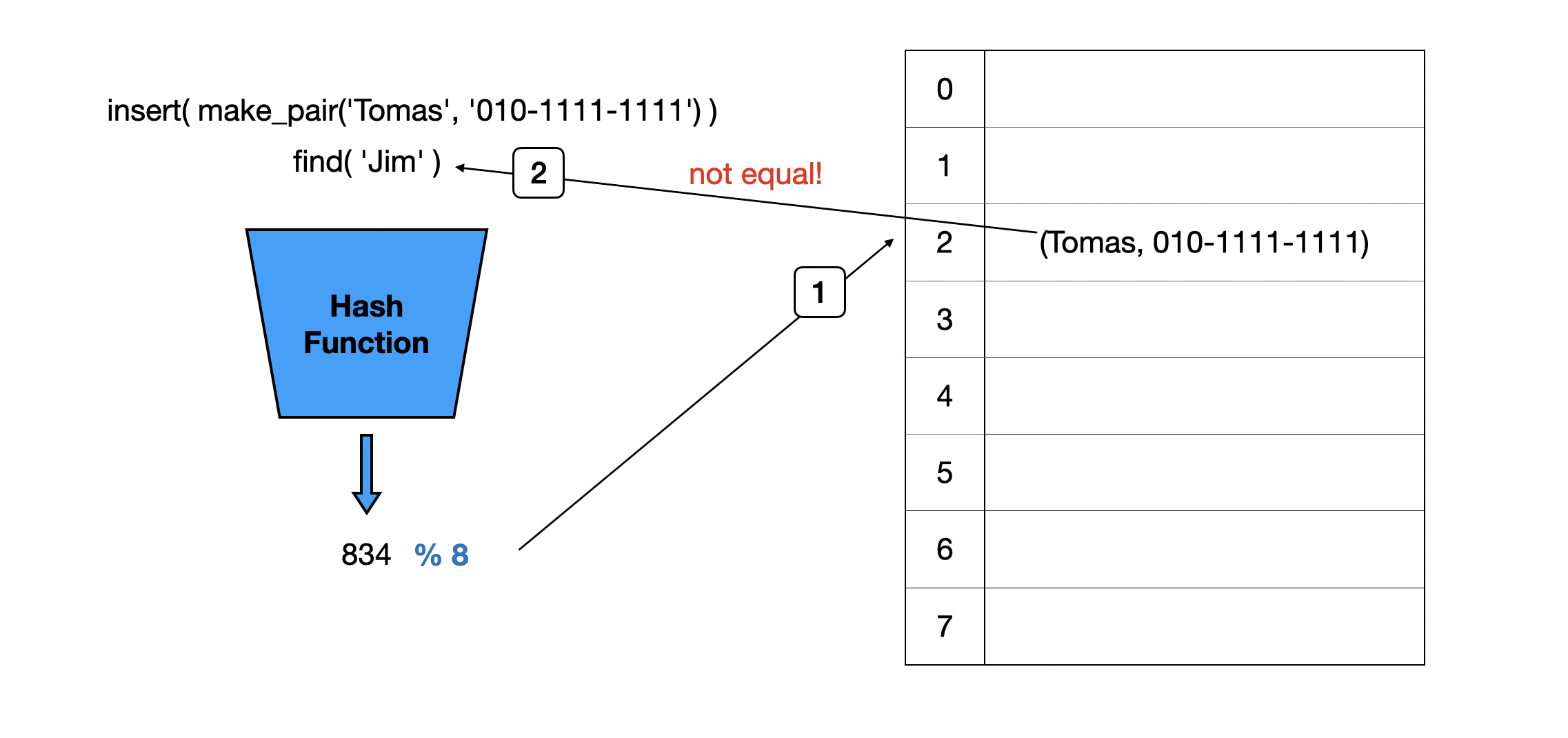
조회한 데이터의 key값인 Tomas가 Jim과 일치하지 않으면 find를 종료할 수 있습니다. 이러한 상황을 Hash Collision이라고 합니다.

Hash Collision

Hash Collision(해시 충돌)은 key는 다른데 hash가 같을 때 발생합니다. 해시 충돌을 아에 막기란 어렵습니다. 보통 저희가 가진 key값보다 capacity의 값이 작기 때문입니다. 또는 key(Tomas, Jim)와 hash(202, 834)도 다른데 hash % capacity(2)가 같을 때 발생합니다.

해시 충돌은 말했듯이 피할 수는 없지만, 이를 대처하는 방법은 있습니다.

Hash Collision 해결 방법

해시 충돌 해결 방법은 대표적으로 Separate Chaining과 Open Addressing이 있습니다.

1. Separate Chaining

먼저 Separate Chaining 방식을 살펴보겠습니다. Separate Chaining은 버킷을 Linked List로 관리합니다.

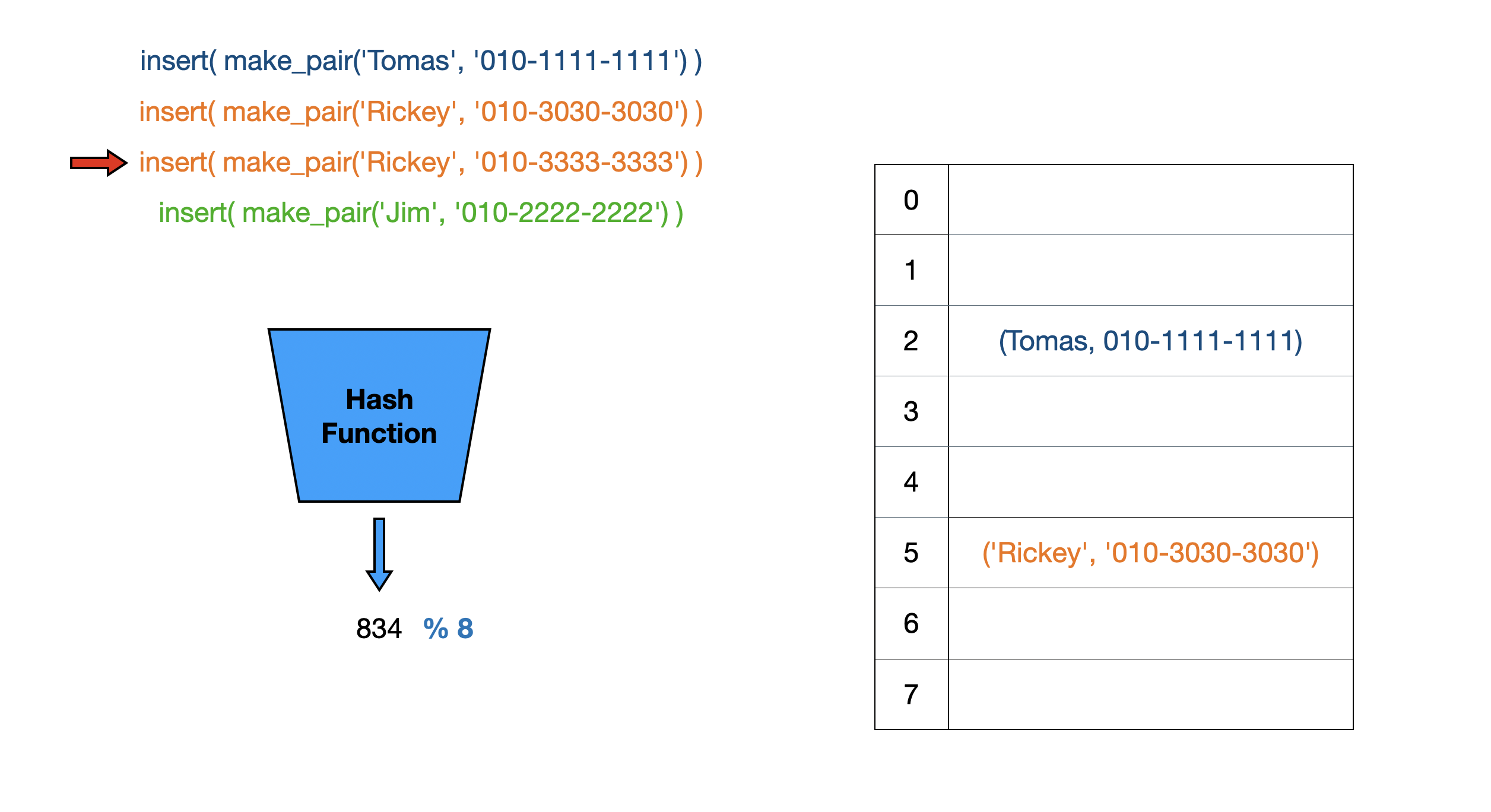
현재 Tomas와 Rickey의 전화번호가 저장되어 있습니다. 그러나, Rickey의 전화번호를 잘못 저장해서 올바른 전화번호를 입력하려고 합니다. ‘Rickey’에 해시 함수와 모듈러 연산을 수행하면 똑같이 5가 나오는데 배열의 5 index에 있는 key값이 ‘Rickey’로 일치합니다. 이런 경우에는 value를 갱신해줍니다.

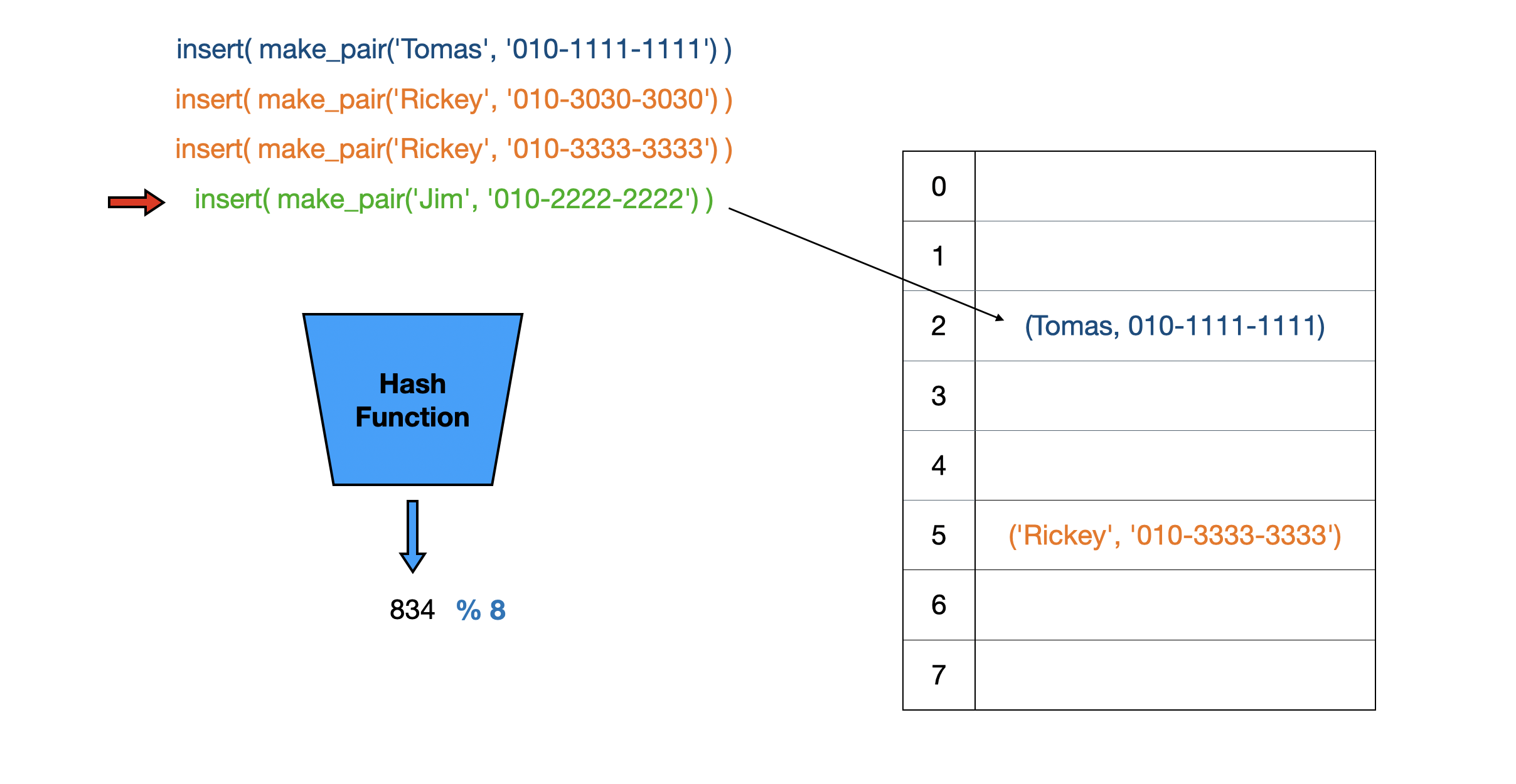
Rickey의 전화번호를 갱신한 뒤 Jim의 전화번호를 입력하려는데 해시 충돌이 발생했습니다.

key값도 다름을 확인하였으니 Separate Chaining 방식은 Linked List로 Jim의 정보를 저장하는 노드를 만들어 버킷이 이를 가리키게 만듭니다.

key값을 조회할 때 만약 해시 충돌이 발생한 버킷이라면 Linked List를 순회하며 Node의 key값이 조회하려는 key값과 같은지 확인합니다.

만약 삭제연산을 진행할 때 해시 충돌이 발생하지 않은 버킷이면 단순히 버킷을 비워주면 되지만, 해시 충돌이 발생한 곳이라면 Linked List의 삭제 연산을 수행해야 합니다.

2. Open Addressing (Linear Probing)

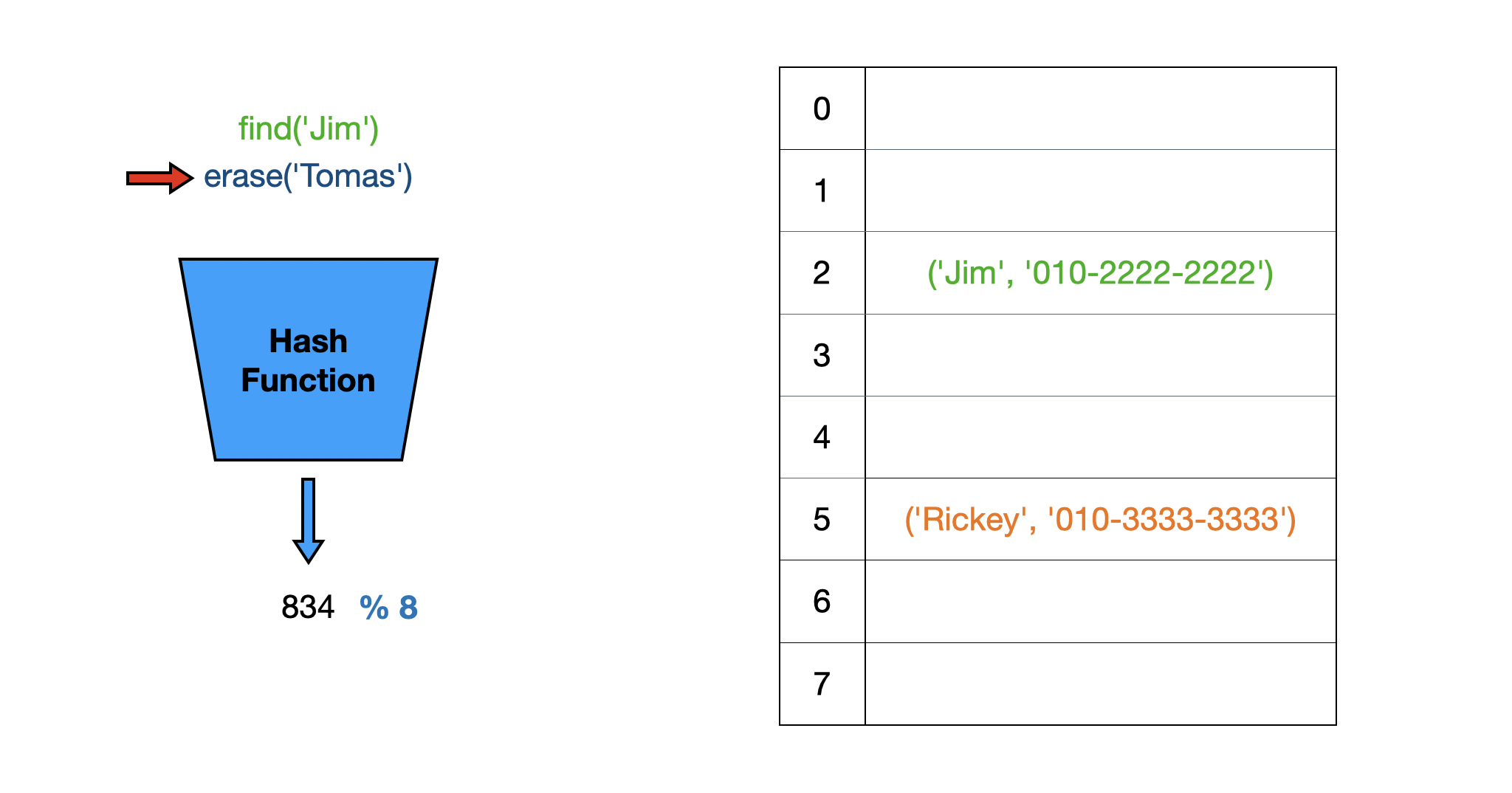
다음은 Open Addressing 중 Linear Probing 방식에 대해 알아보겠습니다.

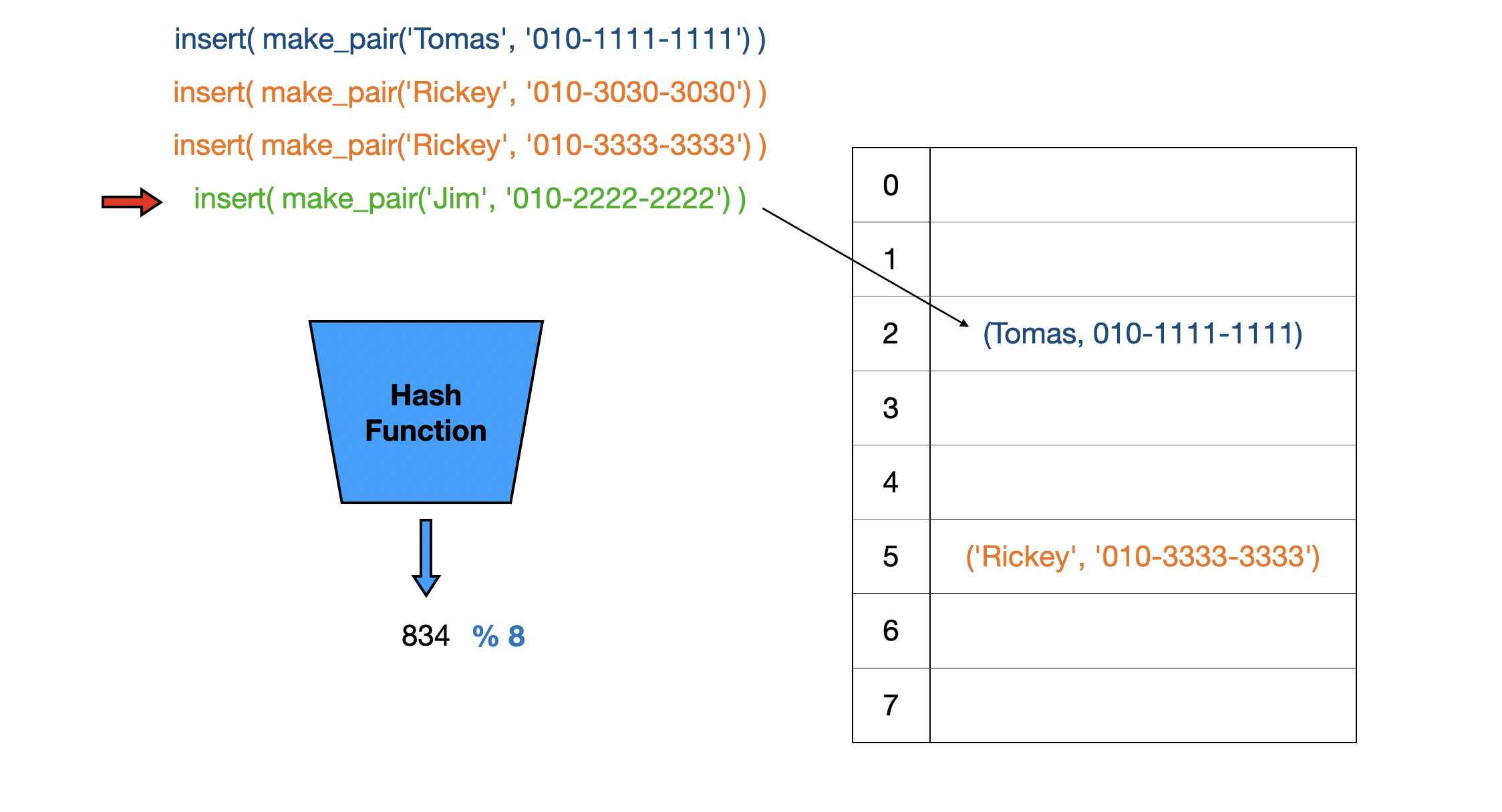
그림처럼 충돌이 발생했을 때, Open Addressing은 비어 있는 버킷을 활용합니다. Linear Probing은 충돌한 버킷의 바로 다음 버킷이 비어있는지 확인한 후 비어있다면 그곳에 저장합니다.

key조회 연산은 어떻게 수행될까요? 버킷의 key가 조회하려는 key와 다르다고 멈추는 것이 아니라 Linear Probing방식에 따르면 다음 버킷에 있을 가능성도 고려해야 합니다. 따라서, 비어 있는 버킷이 나올때 까지 다음 버킷을 순회하게 됩니다.

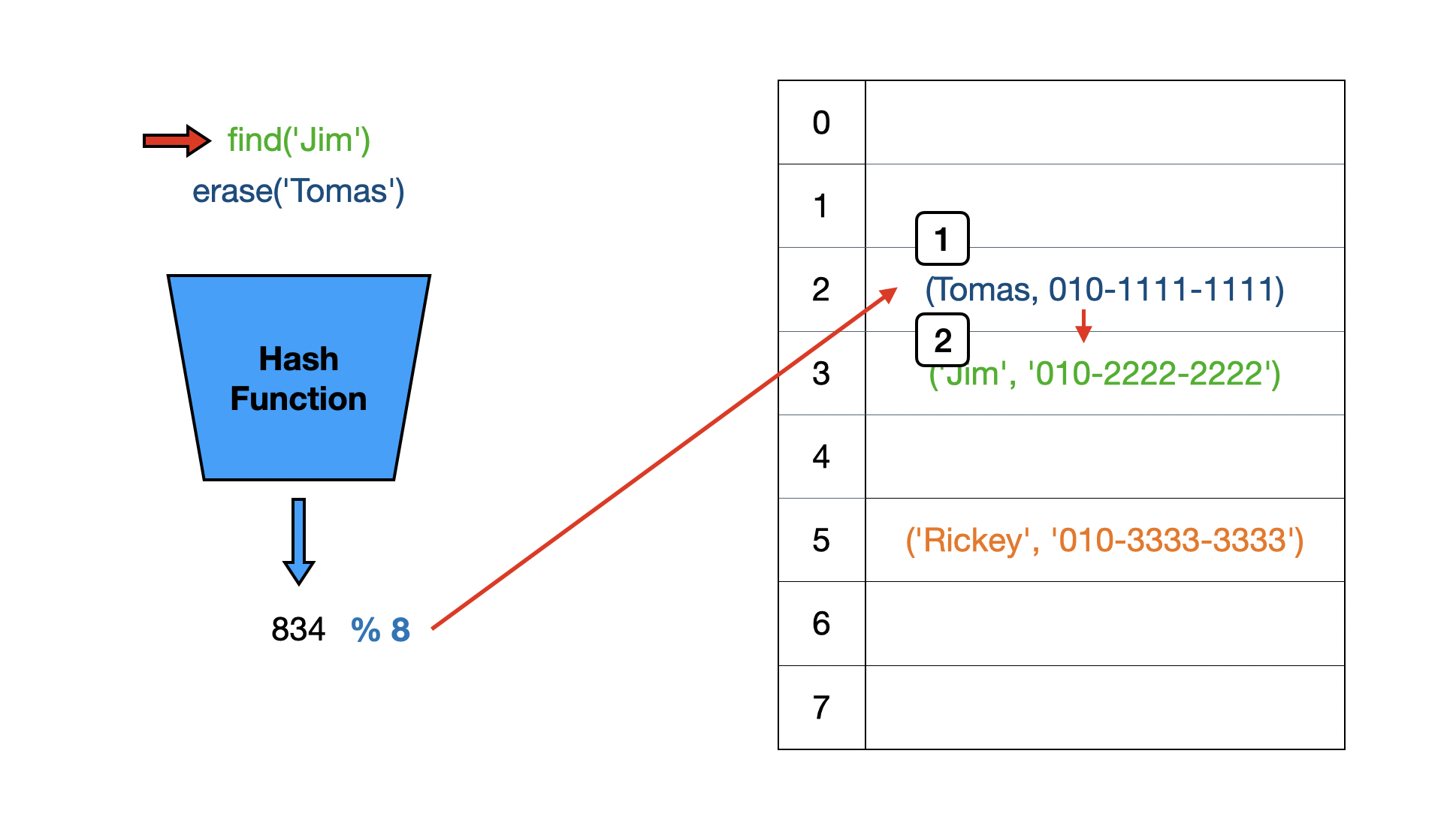
Linear Probing 방식에서 단순히 버킷을 비우면 될까요?

이 상황에서 Jim을 다시 조회한다면 버킷이 비어있기 때문에 다음 버킷을 순회하지 않고 연산을 종료해버리게 됩니다. 배열엔 Jim이 있지만, 찾을 수 없는 상황이 발생합니다.

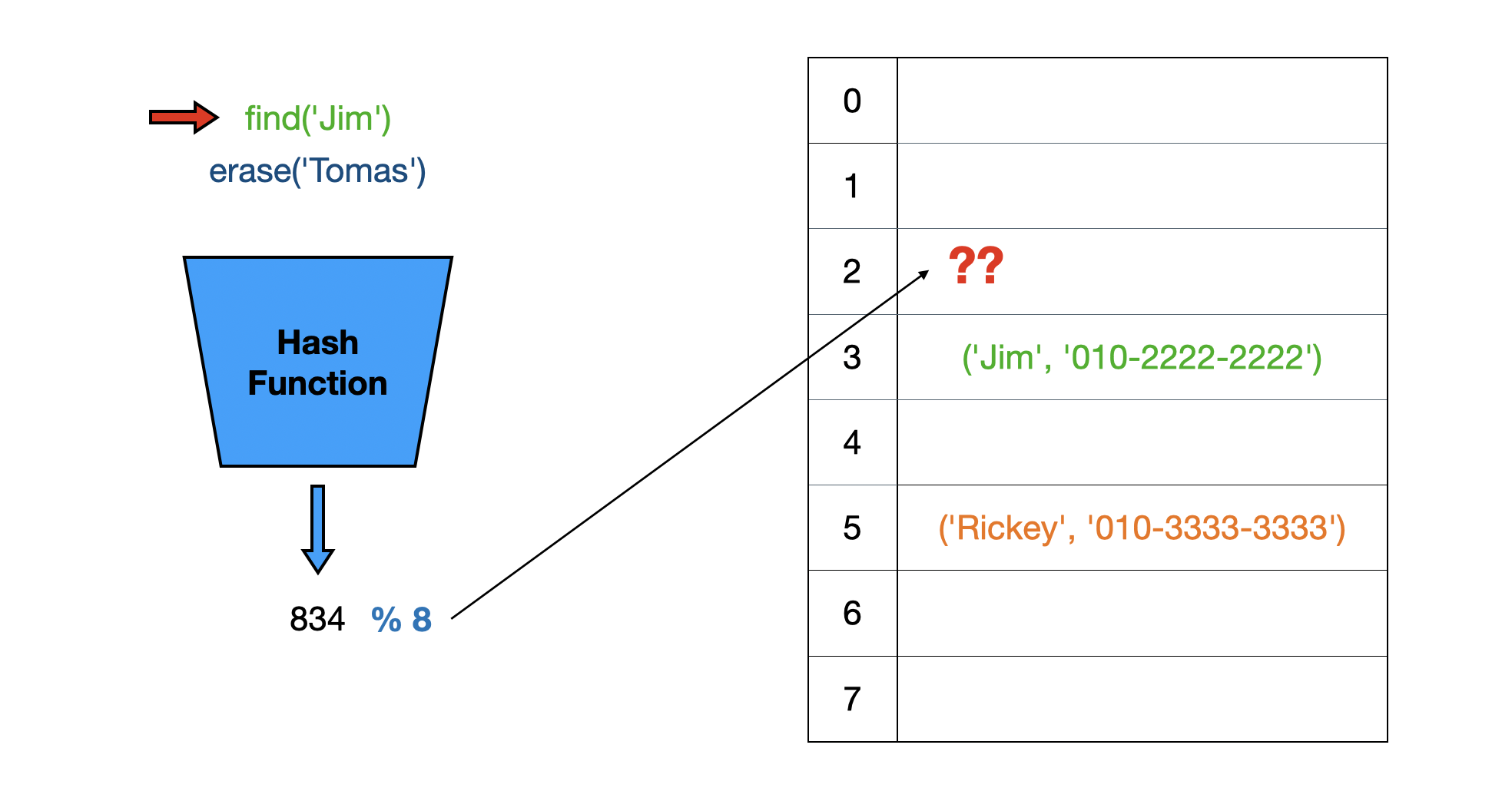
따라서, 단순히 버킷을 비우는 것이 아니라 여기에 값이 있었다라는 정보를 더미 데이터로 놔둬야 합니다.

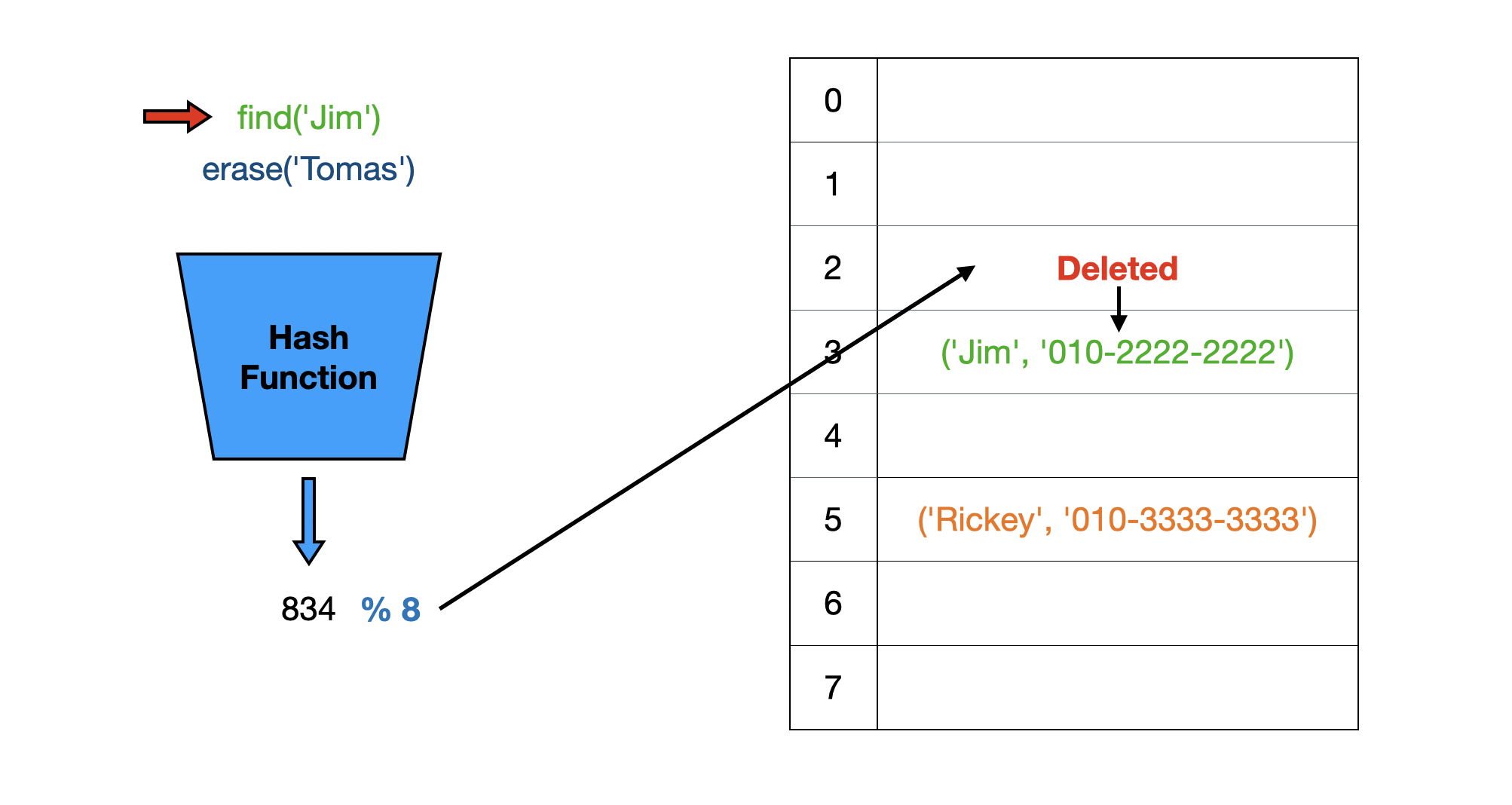
그래야 key를 조회할 때 버킷에 deleted가 있다면 다음 버킷에 찾고자 하는 데이터가 있을 가능성을 고려할 수 있습니다.

Hash Table Resizing

데이터를 많이 저장하다보면 해시 충돌이 많이 발생하게 되고 삽입 및 조회, 삭제 과정에서 더 많은 시간 비용을 요구하게 됩니다. 따라서 해시 테이블의 이점을 잃어버리기 때문에 데이터가 많이 차게 되면 배열의 크기를 늘려줘야 합니다.

Java의 경우 map 배열의 75%가 차면 capacity를 2배로 늘려줍니다.

Linear Probing 방식의 Resizing 과정

실제로 Linear Probing 방식에서 resizing이 일어나는 과정을 살펴보겠습니다.

capacity가 8인 배열에서 capacity가 16인 배열로 버킷들을 옮겨야 하는 상황입니다. 이때 각각의 key값에 대하여 해시 함수를 다시 수행해야 할까요? 그렇게 되면 resizing의 수행 시간이 많이 늘어날 것으로 예상됩니다.

이를 위해 처음 데이터를 저장할 때 계산한 hash값도 같이 저장해야 합니다. 그러면 resizing이 발생할 때마다 일일이 해시 함수를 수행하지 않아도 됩니다.

저장해놨던 해시값에 16만큼 모듈러 연산을 수행한 뒤 2배 늘어난 map 배열에 저장한 결과입니다.

좋은 Load Factor는 몇인가?

Load Factor란 map 배열에 데이터가 얼마나 저장되어 있을 때 resizing을 수행해야 하는지에 대한 인수입니다. Load Factor가 0.75라면 데이터가 75%만큼 차 있을 때, map 배열의 capacity를 늘려야 합니다.

그렇다면 Load Factor를 몇으로 둬야 효율적일까요?

극단적으로 생각하여 Load Factor가 매우 낮다면, map 배열의 공간을 적극적으로 활용하지 못합니다. 많은 버킷들이 비어있는 상태로 존재하게 되죠. 또한, resizing이 빈번하게 일어납니다.

만약 Load Factor가 매우 높다면 공간을 적극적으로 활용할 수는 있지만 해시 충돌 확률이 늘어나게 됩니다. 해시 충돌이 많이 발생한 경우에는 삽입, 조회, 삭제 연산 수행 시간이 늘어나게 됩니다. resizing은 Load Factor가 낮을 때 보다 자주 일어나지 않습니다.

Load Factor에 따른 배열이 비어있는 정도 및 충돌 발생 횟수가 다음 처럼 그래프가 형성됩니다.

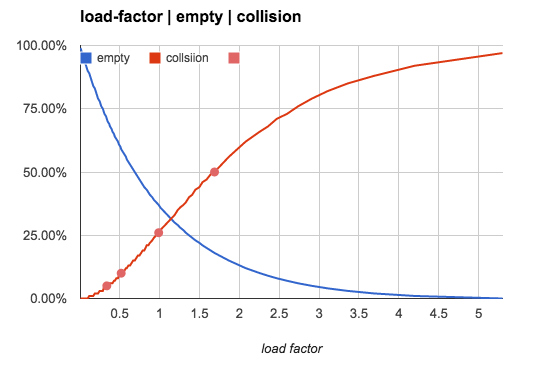
As a general rule, the default load factor (.75) offers a good tradeoff between time and space costs. Higher values decrease the space overhead but increase the lookup cost (reflected in most of the operations of the HashMap class, including get and put). The expected number of entries in the map and its load factor should be taken into account when setting its initial capacity, so as to minimize the number of rehash operations. If the initial capacity is greater than the maximum number of entries divided by the load factor, no rehash operations will ever occur.

Java docs에서는 0.75가 시간과 공간 비용 사이의 가장 양호한 tradeoff를 제공한다고 말합니다.

해시 함수가 얼마나 해시 충돌을 막아주느냐에 따라 다르겠지만, 결국 공간의 활용도와 삽입, 조회, 삭제 연산 시간 및 resizing 횟수를 고려하였을 때 적절한 Load Factor는 0.75라고 볼 수 있습니다.